Equal Area Criterion
To determine the maximum permissible increase in mechanical power input for system stability.
Last Updated: November 01, 2025
Version: 1.0.0
Generated: December 04, 2025
Definition in a Textbook
Source:
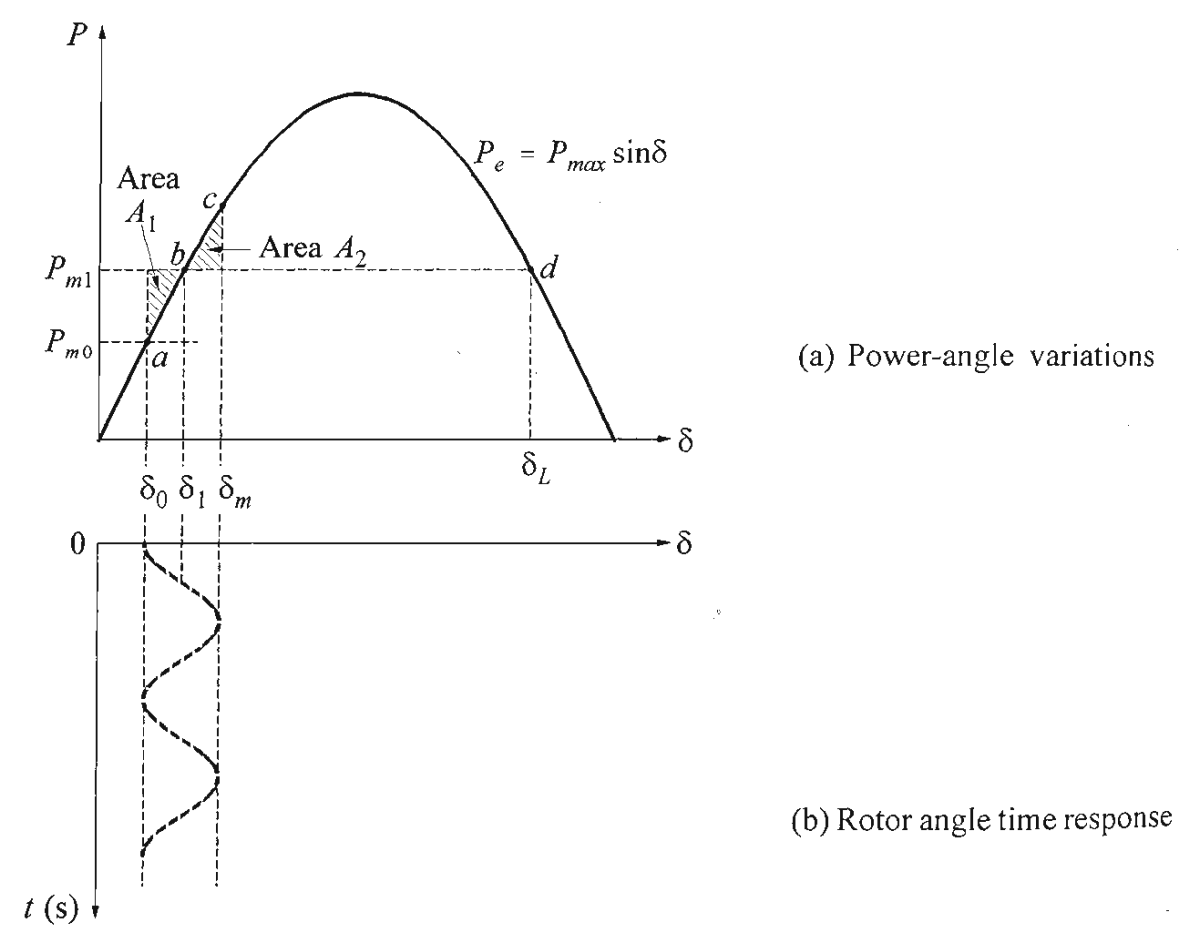
The equal-area criterion is useful in determining the maximum permissible increase in $P_{m}$ for the system illustrated in Figure 13.14. Stability is maintained only if an area $A_{2}$ at least equal to $A_{1}$ can be located above $P_{m}$. If $A_{1} > A_{2}$, then the rotor angle $\delta$ will exceed its critical value, and stability will be lost. For $\delta > \delta_{\max}$, $P_{m}$ exceeds $P_{e}$, leading to net acceleration rather than deceleration.
Another earlier reference to the Equal Area Criterion can be found in